| Teacher | What number is root 18? |
| Students | Between 4 and 5. |
| Teacher | Who wants to explain? |
| Gail | 4 squared is 16 and 5 squared is 25. |
| Teacher | Who is it closer to? [1] |
| Dina | To 4. |
| Teacher | To 4. Because? |
| Dina | 18 is closer [pause] |
| Teacher | Because 18 is closer to 16 than to 25. |
| Dina | It’s 2 [away from 16] and it’s 7 [away from 25], the difference. |
This transcript, from an eighth grade mathematics class in Israel, was viewed in a video-based professional development course. At the time it did not elicit a response from the participating teachers, yet for us something about the reasoning did not feel quite right. Clearly the claim (C) “√18 is closer to 4 than to 5” is correct, and so is the data (D) on which it relies “18 is closer to 16 than it is to 25”, but is it correct to say that C is true because of D?
We acknowledge that different mathematical communities, each guided by their particular mathematical norms and goals, may have different reasons for endorsing or rejecting D as the cause of C. Research mathematicians typically engage in routines of proving; for them, D might be said to cause C if it is a key element in a proof of some generalization of C. Eighth grade students often engage in routines of calculation and estimation. They might sense that 18’s proximity to 16 is in some sense ‘responsible’ for √18’s proximity to 4, and that this supports estimation. Teachers, in deciding whether or not to endorse such a narrative in their classroom, might be guided by what their students currently know and what they need to know in the near future. Hence, we must give up the fallacy of an ‘objective’ analysis of the statement. Instead, we consider the perspectives of research mathematicians, eighth grade learners of mathematics and their teachers on the meaning of the word ‘because’ in argumentation.
Our initial motivation was to map out the potential of this teaching vignette for fueling a discussion in professional development courses. Our analysis of the statement revealed unexpected depth and nuance, both mathematical and pedagogical. In this article we reconstruct our analysis with two goals in mind. The first is to share our findings regarding the particular mathematical issue at stake and regarding mathematical argumentation in different communities. The second is to demonstrate how a multi-faceted analysis of an apparent error can serve as a springboard for investigation. Furthermore, we show how the mathematical and pedagogical perspectives interact and enrich each other.
Theoretical background
We conceive of mathematical ‘knowledge’ as a particular community’s discourse—its established modes of communication—which are constituted in keywords and their use, in narratives that are endorsed or rejected by the community, in useful visual mediation, and in repetitive routines (Sfard, 2008). The community of research mathematicians defines a particular mathematical discourse. However, there are other communities that engage in mathematical discourse, such as school teachers, and researchers in the field of mathematics education. Even an individual mathematics classroom may have its own particular discourse. Communities may differ in their use of common keywords, in the types of routines they engage in, or in the rules and norms that determine which narratives will be endorsed and which will be rejected.
An argument is a particular type of narrative, and argumentation is a particular type of discursive routine. According to Toulmin’s (1958) model for the structure and the semantic content of argumentation, an argument will typically consist of a claim (or conclusion) based on data, and a warrant that entitles one to draw the conclusion from the data. Additionally, it may include backing on which the warrant relies, a qualifier expressing degrees of the arguer’s confidence in the conclusion, and a rebuttal that consists of potential refutations of the conclusion, including exceptions or conditions under which the conclusion would not hold. In these terms, the claim “√18 is closer to 4 than to 5” is based on data “18 is closer to 16 than it is to 25”. In the background lurks a tacit warrant about which we may hypothesize. Perhaps the arguer’s warrant was “whenever a number is closer to n2 than it is to (n + 1)2 , its root is closer to n than it is to n + 1”. Warrants, and in particular the backings on which they rely, depend on the field of activity in which the argumentation is taking place. From our discursive perspective we would replace the term field with discourse. For example, in the discourse of research mathematicians, a backing for the above warrant would typically be that it can be proven.
Freeman (2005) finds Toulmin’s notion of field dependence problematic. He claims that individuals may partake in many fields of activity, and that it is often difficult (and unproductive) to attempt to determine the field in which argumentation is taking place. Instead, he classifies warrants based on the type of intuition, belief or prior understanding that gave rise to them. He has proposed four categories: a priori (based on primary intuition), empirical (based on experience or secondary intuition), institutional (based on definitions or on defining rules) and evaluative (requiring an argumentation process such as mathematical proof).
This classification preserves Toulmin’s insight on the field dependency of warrants but without the problematic notion of field. Different warrants will be justified or backed in different ways, and we must look to the type of warrant to determine how this is done properly. (p. 342).
Von Glasersfeld (1993) has argued that, “Whatever a student says […] is what makes sense to the student at that moment. It has to be taken seriously as such, regardless of how odd or ‘wrong’ it might seem” (p. 10). Applying this to argumentation, we recognize a pedagogical implication of Freeman’s approach. From Toulmin’s perspective, considering fields of activity may lead us to decide whether an argument is valid, or normative ( i.e., would be endorsed by a particular community), whereas considering the type of intuition or prior understanding that an argument relies on, suspending the question of whether it is ‘valid’, may help us make sense of student thinking.
Chazan & Herbst (2012) have used breaching experiments to investigated mathematics teachers’ norms, both mathematical and pedagogical. By showing teachers classroom vignettes that may feel ‘not quite right’ to some of them, they elicit and reveal tacit classroom norms. In these terms, the claim about √18 may be said to have breached a tacit norm of our mathematical discourse. A goal of this study is to make our breached mathematical norms explicit, first to ourselves and then to readers of this paper, in revealing why we tend to reject the statement about √18. Yet we realize that this statement may make sense to others. Moreover, even if we do eventually reject the statement, reflecting upon it may still prove productive. Borasi (1996) has suggested how classroom errors may serve as springboards for mathematical investigation. Drawing on this, we suggest how an argument, deemed an error, may serve as a springboard for mathematical and pedagogical investigation in teacher education. Here we model such an investigation.
Epistemic analysis: the mathematician’s perspective
We consider the following statement, based on the exchange that took place in the eighth grade class:
Statement 1.1: √18 is closer to 4 than to 5 because 18 is closer to 16 than it is to 25.
Our goal in this section is to elaborate our norms of argumentation (as mathematicians), by explicating in what sense this statement breached them. For this we elaborate the statement with hypothetical arguments, and discuss reasons for endorsing or rejecting each of them.
In the discourse of research mathematicians, the word ‘because’ in Statement 1.1 should be related to the idea of mathematical proof. We present a hypothetical argument, following Toulmin’s structural decomposition into claim, data, warrant and backing:
Argument 1.1: (Claim:) √18 is closer to 4 than to 5, because (Data:) 18 is closer to 16 than it is to 25, since (Warrant 1.1:) whenever a number x is closer to 16 than it is to 25, √x is closer to 4 than it is to 5, on account of the fact that (Backing 1.1:) Warrant 1.1 can be proven.
In this we have made explicit a possible meaning of ‘because’ in Statement 1.1. Thus, we must decide if Warrant 1.1 can be proven. This suggests an investigation.
Investigation 1.1: Prove or refute Warrant 1.1.
The outcome of this investigation is that Warrant 1.1 is invalid, since, for example, 20.3 is closer to 16 than it is to 25, yet √(20.3) ≈ 4.505 is closer to 5 than it is to 4. We note that the range of counterexamples is rather small: the interval 20.25 < x < 20.5 of length 0.25.
We have shown a sense in which Argument 1.1 can be considered invalid. It implicitly relies on Warrant 1.1, which is not provable, having a counterexample.
It seems that we have revealed the source of our unease regarding Statement 1.1, however we claim that the situation is more delicate, and demonstrate this by suggesting a similar line of argumentation using different numbers. Suppose the statement had been:
Statement 1.2: √21 is closer to 5 than to 4 because 21 is closer to 25 than it is to 16.
This statement could be argued as follows:
Argument 1.2: (Claim:) √21 is closer to 5 than to 4, because (Data:) 21 is closer to 25 than it is to 16, since (Warrant 1.2:) whenever a number x is closer to 25 than it is to 16, √x is closer to 5 than it is to 4, on account of the fact that (Backing:) Warrant 1.2 can be proven.
This argument suggests a new investigation:
Investigation 1.2: Prove or refute Warrant 1.2.
Unlike warrant 1.1, Warrant 1.2 can be proven, as follows. Assume that x is greater than
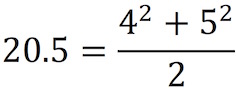
Then it is also greater than
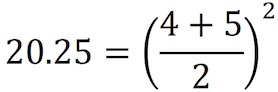
and since the root function is increasing, √x > 4.5 will hold.
Would Argument 1.2 be endorsed by the community of research mathematicians? Warrant 1.2 is provable, and the claim follows from the data based on the warrant, hence based on the discussion above the answer should be ‘yes’. Yet we wonder, is Warrant 1.2 appropriate? Is the data really the cause of the claim? We hope readers share our feeling that this is still not quite right, and we will try to articulate why.
Expectations from the keyword ‘because’: In the discourse of research mathematicians, much as in more general discourse, an argument phrased as ‘Claim because Data’ should not only convince us that the claim is true, but should also provide some insight into the nature of the causality between the data and the claim, as suggested by the word be-cause. From our perspective, Argument 1.2, though based on the provable Warrant 1.2, fails to provide such insight because it remains unclear why, in spite of the similarity between Warrant 1.1 and Warrant 1.2, the second is valid and the first is not.
Generality : To understand why √21 is closer to 5 than it is to 4, and why √18 is closer to 4 than it is to 5, we would like a general warrant. Warrants 1.1 and 1.2 feel a bit too particular. To begin with the roles of the numbers 4, 5, 16 and 25 could be generalized to n, n + 1, n2, (n + 1)2 but even then, the occurrence of two similar claims (Warrants 1.1 and 1.2), with one valid and the other not, suggests that a more general pattern is waiting to be discovered.
Both concerns would be resolved if the following generalized warrant were valid:
Warrant 1.3: If a number x in the interval [n2, (n + 1)2] is closer to one of the endpoints, √x is closer to the corresponding endpoint of the interval [n, n + 1].
We already established, that as stated, Warrant 1.3 is invalid. However, we now suggest the following investigation:
Investigation 1.3: Find all counterexamples for Warrant 1.3. Modify it to make it provable, and rephrase Statement 1.1 accordingly.
This investigation yields a result that we found surprising. The warrant is ‘almost valid’ in the sense that the range of counterexamples, the interval n2 + n + ¼ < x < n2 + n + ½, is of length 0.25 for any n, as it was in the particular case of n = 4, and the relative range of counterexamples 0.25/((n+1)2 – n2) tends to zero. Thus, Warrants 1.1 and 1.3 could be ‘fixed’ by adding an appropriate rebuttal. We would suggest the following:
Statement 1.4: √18 is closer to 4 than to 5 because 18 is much closer to 16 than it is to 25.
Warrant 1.4: If a number x in the interval [n2, (n + 1)2] is sufficiently close to one of the endpoints, √x is closer to the corresponding endpoint of the interval [n, n + 1].
We will elaborate on this statement and its warrant in the following section.
Pedagogical analysis: the student’s and the teacher’s perspectives
Statement 1.1 was produced by a student, while guided and encouraged by a teacher. Accepting von Glasersfeld’s stance, this statement must have made sense to the student (and to the teacher). We wish to investigate what sense we can make of the statement from the student’s perspective. Our aim is not to get to the bottom of a particular student’s thinking, but rather to harness this pedagogical stance, considering what the student may have been thinking, for our inquiry into epistemic and pedagogical aspects of the mathematics at hand.
To begin with, the mathematics practiced in eighth grade classrooms is different from what is practiced in mathematics departments. For a mathematician, the particular value of √18 is of little interest; the main issue is the provability of the warrant’s general claim. However, in many school contexts, estimating the value of a calculation is a valued routine, and any argument supporting Statement 1.1 should be considered in this context. In Toulmin’s terms, the student’s argument and the mathematician’s argument belong to different fields of activity.
To makes sense of the student’s statement it is not sufficient to consider her field of activity; we appeal additionally to Freeman’s categories of argumentation. Consider the following hypothetical argument:
Argument 2.1: (Claim:) √18 is closer to 4 than to 5, because (Data:) 18 is closer to 16 than it is to 25, since (Warrant 2.1:) whenever a number x is close to n2, √x is close to n.
Such a warrant, with or without a rebuttal (conditional on how close x is to n2), appears to be appropriate for estimating √18. What might its backing be? We propose the following:
…on account of the fact that (Backing 2.1:) this is my experience of the root function.
In Freeman’s terms, we are suggesting that unlike the mathematician’s backing, which was evaluative (i.e., based on the provability of the warrant), a student’s backing for Warrant 2.1 may be empirical ( i.e., based on experience), since the warrant may be a means toward the goal of approximating a calculation. This leads us to a crucial pedagogical question: what eighth grade prior understandings of the root function can back Warrant 2.1? Different schooling contexts may suggest different answers. Hence, the inquiry we are suggesting may differ across different contexts. We suggest answers based on our experience with schooling in Israel.
Our first answer is continuity. Though students have not been formally introduced to this notion, it underlies the view that 18’s proximity to 16 ‘causes’ √18’s proximity to 4. Yet, the claim was not just that √18 is close to 4, but closer to 4 than to 5. This appears to be based on a notion of monotonicity. Accordingly, we propose:
Warrant 2.2: As x increases from 16 to 25, √x increases from 4 to 5.
This warrant suggests that there is some point at which √x will make the transition from ‘closer to 4’ to ‘closer to 5’. We feel that such a warrant, coming from a student, would be empirical in Freeman’s terms. It is not a priori (immediately obvious), nor is it institutional (based on rules or definitions), or evaluative (based on some reasoning process). It is based on some secondary intuitions that a student has picked up regarding the root function.
Revisiting Warrant 1.4 with these mathematical ideas in mind, we realize that the words ‘much closer’ have sound mathematical meaning, drawn from the definition of (right) continuity: for any ε > 0 there exists δ > 0 such that x – 16 < δ ⇒ √x & 4 < ε. In these terms, Statement 1.1 tacitly relies on the understanding that δ = 2 is an appropriate value for ε = 0.5.
We now consider Statement 1.4 (based on the data that 18 is much closer to 16) with Warrant 2.2 in mind. We feel that this statement would be endorsed by research mathematicians and teachers alike, since the argument it suggests is quite sophisticated. Its warrant is still empirical, relying on experience of functions that are continuous and monotonic[2], while its rebuttal, implied by the word ‘much’, allows for exceptions further away from 16. Though the word ‘much’ may appear rather vague, anyone familiar with the mathematician's discourse knows how to formalize it into an evaluative argument, based on the following:
Warrant 2.3: There exists a unique number 16 < d < 25 such that for every 16 ≤ x ≤ 25: If x < d then √x is closer to 4 than to 5, and if x > d then √x is closer to 5 than to 4.
This suggests a variation on Investigation 1.3:
Investigation 2.1: Find d for which Warrant 2.3 holds, and generalize.
Warrant 2.3 is attractive from a mathematician’s perspective because it not only generalizes the role of 18 to any number sufficiently close to 16, it also suggests a generalization of the role of the root function to any function that is continuous and monotonic on some interval.
We now give Warrant 2.2 and its backing more careful scrutiny. Where might a student’s experience of continuous and monotonic functions originate? The way Statement 1.1 is phrased suggests to us that the speaker believed (mistakenly) that the transition of √x from closer to 4 to closer to 5 takes place exactly midway between 16 and 25. It seems likely that the student, and possibly even the teacher, were applying linear thinking in a non-linear situation (see for example Markovits, Eylon, & Bruckheimer, 1983). Clearly if f(x) is linear in the interval [4, 5] (i.e., its graph is a straight line), then the following statement is valid:
Statement 2.2: If a number x in the interval [a, b] is closer to one of the endpoints, then f(x) is closer to the corresponding endpoint of the interval [f(a), f(b)].
The function x2 and its inverse √x are not linear functions, but they have much in common with linear functions (continuous and monotonic). It seems plausible that statement 1.1 was based on an overextension of a principle that is valid for linear relationships. From this perspective even Statement 1.2, argued with the valid warrant 1.2, may be considered ‘pedagogically’ invalid, if we accept that it is based on a misapplication of linearity. This suggests a pedagogical explanation for our unease regarding Statement 1.1; regardless of its epistemic validity, we suspect that it is based on a student misconception, and as such is invalid.
This provides a new perspective on Warrant 1.3 (if x in the interval n2 < x < (n + 1) 2 is closer to one of the endpoints, √x is closer to the corresponding endpoint of the interval [n, n + 1]). Investigation 1.3 called for an evaluative argument for the invalidity of this warrant: finding (and proving) the range of counterexamples. However, we clearly recall the argument that first came to our own minds:
Argument 2.4: (Claim 2.4:) Warrant 1.3 is invalid, because (Data:) it would have been valid if √x were linear, but it is not.
What kind of warrant might this argument rely on? We noted that Statement 2.2 holds for linear functions, where the transition from “closer to f(a)” to “closer to f(b)” occurs at the midpoint (a + b)/2. Moreover, this property appears to characterize linear functions (i.e., is a necessary and sufficient condition for linearity). Thus, we suggest the following:
Warrant 2.4: If a property characterizes linear functions, then it does not hold for non-linear functions.
Warrant 2.4 implies that if f(x) is not linear, then the point d (as in Warrant 2.3) cannot be the midpoint of [16, 25], and Claim 2.4 follows from the data based on this warrant. The problem is that Statement 2.2 is not a sufficient condition for linearity! This can be ascertained through the following investigation:
Investigation 2.3: Find a non-linear continuous increasing function for which Statement 2.2 holds.
We demonstrate the existence of such functions in the next section, on the student’s perspective.
A note on the teacher’s perspective : Our epistemic and pedagogical analysis may cause one to question the teacher’s wisdom in eliciting and endorsing Statement 1.1. However, she may have been able to warrant this teaching move pedagogically. It is beyond the scope of this article to propose such pedagogical warrants. We refer readers to the work of Nardi, Biza, and Zachariades (2012), who have drawn on the works of Toulmin and of Freeman to study teachers’ warrants, distinguishing between epistemological/pedagogical, a-priori/empirical/institutional/evaluative and personal/professional considerations in their argumentation.
Returning to the epistemic analysis from a student’s perspective
Our first epistemic analysis was based on evaluative argumentation: warrants that are mathematically provable. We now return to an analysis of the mathematics, focusing on mathematical understandings and intuitions that students may bring, including notions of continuity, monotonicity and linearity. We begin by working out a generalization of investigation 1.3.
Investigation 3.1: Prove or refute the following claim: If a number in the interval (a2, b2) is closer to one of the interval’s endpoints, its square root is closer to the corresponding endpoint of the interval (a, b).
To refute this claim by counterexample, one must find a number y for which one of the following holds:
A. y is closer to a2, i.e., y < (a2 + b2)/2, yet its root is closer to b, i.e., √y > (a + b)/2
B. y is closer to b2, i.e., y > (a2 + b2)/2, yet its root is closer to a, i.e., √y < (a + b)/2
We have argued for the case a = 4, b = 5 that
counterexamples of type A do exist; For the general case we let
d = b – a
be the length of the interval (a, b). We first find the
midpoint of the interval (a2, b2).
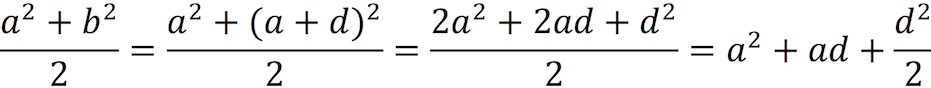
We compare this to the square of the midpoint of the interval (a, b).

Regardless of the values of a and b, there is a difference of exactly d2/4 between these terms. This shows that counterexamples of type B cannot exist, and that counterexamples of type A do exist, and they are all in an interval of length d2/4 satisfying
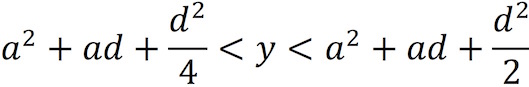
This argument has an enlightening visual representation. Figure 1 shows two points A, B on the parabola y = x2 (or x = √y). Point C is the midpoint of the chord between A and B.

Figure 1. Visual representation of the midpoint argument.
The dashed lines x = (a+b)/2 and y = (a2 + b2)/2 section the plane into four ‘quadrants’. The ranges of counterexamples of type A and B now have a graphic interpretation: a counterexample of type A is a point on the parabola in the lower right quadrant and a counterexample of type B is a point on the parabola in the upper left quadrant. The parabola is convex, its graph is completely below the chord, hence it does not pass through the upper left quadrant, and counterexamples of type B do not exist. The range of counterexamples of type A is indicated in Figure 2.
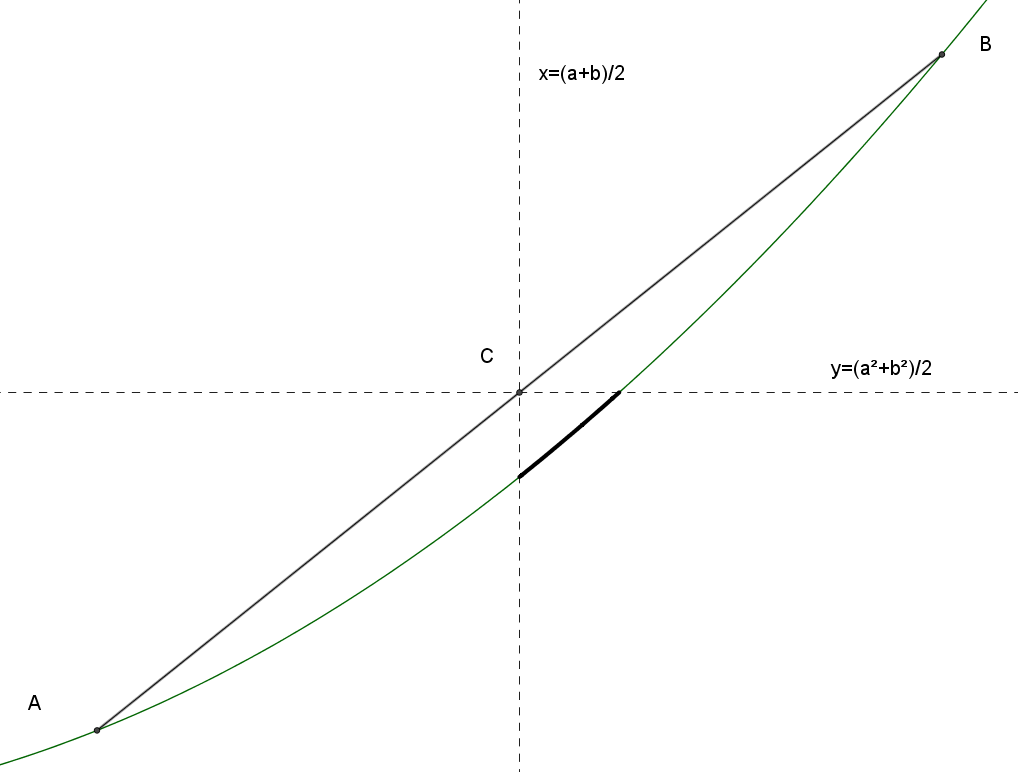
Figure 2. The range of counterexamples of type A.
What might students make of Statement 1.1?
We were curious to know what students would think about Statement 1.1. We did not investigate this systematically, but the first author did pilot this question with his son, a twelfth grade advanced track math student. He, like us, recognized the tacit warrant 1.3 in this statement, which he immediately realized was incorrect. He argued as follows: If warrant 1.3 were true, then it would necessarily be true that “The root of the midpoint is the midpoint of the roots”, i.e.,
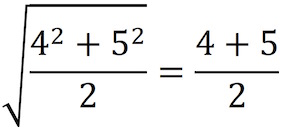
Since this is not the case (√20.5 ≠ 4.5), warrant 1.3 is false and a counterexample must exist. We asked ourselves what understandings this argument might rely on. It seems to be based on a notion of continuity, although the student had no formal knowledge of calculus beyond what is taught in high school. His argument can be formalized (i.e., proven) relying on the intermediate value theorem applied to the continuous function f(x) = √x, however the visualization that we introduced suggests a concrete realization of the intermediate value theorem that may be more readily available for students. The graph of √x passes continuously from the point (4, 16) in the lower left quadrant to (5, 25) in the upper right quadrant. If we assume (by negation) that the graph does not pass through the upper-left or the lower-right counter-example quadrants, it must pass through point C (4.5, 20.5) . Since it does not (√(20.5) ≠ 4.5), Warrant 1.3 is invalid.
Linearity is sufficient for Statement 2.2, but not necessary
We now return to Investigation 2.3, and use our visualization to show a counterexample: a continuous strictly increasing non-linear function for which Statement 2.2 holds. Such a function need only pass through the points (4,16) and (5,25), while remaining outside the two counter-example zones. Clearly such a function need not be linear (see Figure 3).
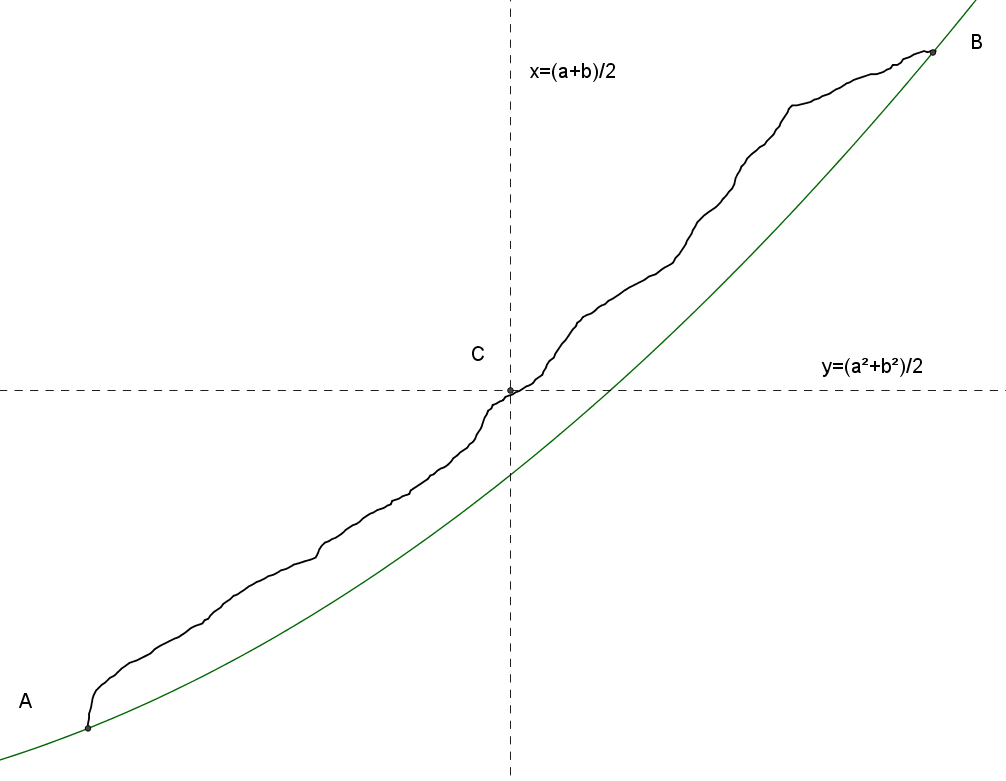
Figure 3. A non-linear function for which Statement 2.2 holds.
As already mentioned, this reveals a flaw in our own reasoning. When we argued in Argument 2.4 that “Warrant 1.3 is invalid because √x is not linear”, we were not allowing for functions such as the one sketched in Figure 3. We wrongly assumed that Statement 2.2 is not only a necessary condition for linearity, but also sufficient. We now apply von Glasersfeld’s principle to ourselves, and see if our mistake may have been based on a productive understanding. We propose that we had the following characterization of linear functions in mind:
Statement 3.1: For any numbers a < b, if a number x in the interval [a, b] is closer to one of the endpoints, then f (x) is closer to the corresponding endpoint of the interval [f(a), f(b)].
This statement is identical to Statement 2.2, except that it is not stated for given numbers a < b, but rather for any numbers a < b. Like Statement 2.2 it is true for linear functions, yet, unlike statement 2.2, it is true only for linear functions [3].
Suppose this had been the argument for Statement 1.1:
Argument 3.1: (Claim:) √18 is closer to 4 than to 5, because (Data:) 18 is closer to 16 than it is to 25, since (Warrant 3.1:) For any numbers 0 < a < b, and for any x in the interval [a, b] if x is closer to one of the endpoints, √x is closer to the corresponding endpoint of the interval [√ a, √b].
This argument is just as mathematically flawed as Argument 1.1, having the same counterexamples for Warrant 3.1 as for Warrant 1.3. However, it has the general flavor that was lacking in previous warrants, where the end points of the interval [a, b] are preceded by the universal quantifier (“for any”). Furthermore, with this argument in mind, we propose a valid version of Argument 2.4:
Argument 3.2: (Claim 3.2:) Warrant 3.1 is invalid, because (Data:) it would have been valid if √x were linear, but it is not. This conclusion is possible since (Warrant 3.2:) if a property is necessary and sufficient for linear functions, then it does not hold for non-linear functions.
Summary
We have reconstructed here our investigation of a mathematical statement from an eighth grade classroom in Israel. We do not claim that students or mathematicians would have argued in the manner we hypothesized. Rather, we have used hypothetical arguments, drawn from our own experience with students and with mathematicians, as objects to reflect on in our analysis.
Our point of departure was an uneasy feeling that the argument was flawed. We began with a mathematical investigation of some hypothetical arguments for the claim. The invalidity of Argument 1.1 seemed to explain our unease, however, the validity of the similar Argument 1.2 encouraged us to dig deeper.
The research mathematicians’ perspective took us only so far. A pedagogical perspective, taking a teacher’s stance and asking ourselves what the speaker may have had in mind, allowed us to make more progress. Possible prior understandings that emerged from this pedagogical perspective, continuity, monotonicity, and eventually linearity, not only shed light on what students might bring to the discussion, but also proved to be productive in our analysis of the underlying mathematics.
Returning to the mathematicians’ perspective with these understandings in mind, we eventually recognized a crucial necessary and sufficient condition of linear functions. This condition suggested a new perspective on the statement: Its argument tacitly relies on a condition that holds only for linear functions. √x is not linear, hence the argument is not valid.
Thus, this necessary and sufficient condition of linear functions (Statement 3.1) emerged as the key for reconciling all of our preceding arguments, evaluative and empirical, epistemic and pedagogical.
Along the way we have explicated our own norms regarding mathematical argumentation, one of which is: Warrants should not only be provable, they should be as general as possible, and should provide some insight into why the argued claim follows from the data. We have also discussed students’ argumentation, which may be based on goals different from the goals of research mathematicians. Furthermore, we have shown that a consideration of students’ prior understandings can shed light not only on their argumentation, but also on the mathematics at stake.
The statement about √18 did not elicit a response from the teachers who witnessed it on video in a professional development course. We suggest that teacher educators should aim at developing the sensitivity and curiosity of teachers to embark on investigations like those we have presented. This requires attentive listening to teachers’ and students’ seemingly obvious mathematical statements during lessons, since they may lead, as in the case of √18, to rich and deep mathematical and pedagogical insights.
Acknowledgements
This paper is based on work which was partially funded by the Israeli Science Foundation (ISF), grant 1539/15, and by the Weizmann Institute of Science. The views expressed in the article reflect those of the authors.
Notes
[1] In Hebrew, as in English, the number would normally be referred to as ‘which’, yet the teacher chose to refer to it as ‘who’.
[2] By monotonic we mean strictly monotonic, here and henceforth.
[3] For lack of space we omit the proof.
References
Borasi, R. (1996) Reconceiving Mathematics Instruction: a Focus on Errors. Norwood, NJ: Praeger.
Chazan, D. & Herbst, P. (2012) Animations of classroom interaction: expanding the boundaries of video records of practice. Teachers College Record, 114(3), 1-34.
Freeman, J. B. (2005) Systematizing Toulmin’s warrants: an epistemic approach. Argumentation, 19(3), 331-346.
Markovits, Z., Eylon, B. & Bruckheimer, M. (1983) Functions: linearity unconstrained. Proceedings of the 7th Conference of the International Group for the Psychology of Mathematics Education , pp. 271-277. Rehovot, Israel.
Nardi, E., Biza, I.. & Zachariades, T. (2012) ‘Warrant’ revisited: integrating mathematics teachers’ pedagogical and epistemological considerations into Toulmin’s model for argumentation. Educational Studies in Mathematics, 79(2), 157-173.
Sfard, A. (2008) Thinking as Communicating: Human Development, the Growth of Discourses, and Mathematizing . Cambridge, UK: Cambridge University Press.
Toulmin, S. E. (1958) The Uses of Argument. Cambridge, UK: Cambridge University Press.
von Glasersfeld, E. (1993) Questions and answers about radical constructivism. In K. G. Tobin, The Practice of Constructivism in Science Education, pp. 23-38. Hilsdale, NJ: Lawrence Erlbaum Associates, Inc.